设f(n)为n个节点的二叉树个数,g(n)为n个节点的二叉树的叶子数量之和。则答案为g(n)/f(n)。
显然f(n)为卡特兰数。有递推式f(n)=Σf(i)f(n-i-1) (i=0~n-1)。
类似地,左子树节点数为i时右子树有f(n-i-1)种情况,那么可以对左子树的叶子节点数之和计数,显然再乘2就是总数了。有递推式g(n)=2Σg(i)f(n-i-1) (i=0~n-1)。
因为递推式是卷积形式,考虑生成函数。设F(x)、G(x)分别为f(n)、g(n)的生成函数(均为无穷级数)。则有F(x)=xF2(x)+1。乘x是为了给他进一位。因为f(0)=f(1)=1,只要补上x^0位上的1就好了。解得F(x)=[1±√(1-4x)]/(2x)。其中√1-4x可以用广义二项式定理计算出来,发现其每一项都是负数,于是我们取F(x)=[1-√(1-4x)]/(2x)。
同样的道理,G(x)=2xF(x)G(x)+x。因为g(0)=0,g(1)=1,进一位后需要补上x^1位上的1。解得G(x)=x/√(1-4x)。
有了生成函数我们可以暴推原数列了。
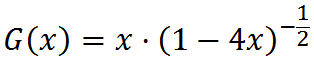
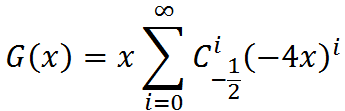
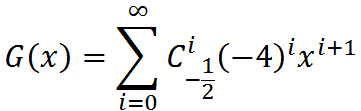
即g(n)=C(-1/2,n-1)·(-4)n-1。这个式子得化的更好看一点。不妨展开组合数。
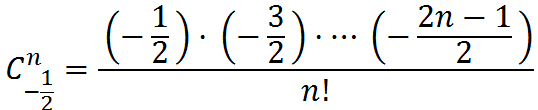
则C(-1/2,n)=(2n)!/(2n·n!)·(-1/2)n/n!=(-1/4)n·(2n)!/n!/n!=(-1/4)n·C(2n,n)。
g(n)=(-1/4)n-1·C(2n-2,n-1)·(-4)n-1=C(2n-2,n-1)。简直优美到爆炸!
我们知道卡特兰数的通项公式是f(n)=C(2n,n)/(n+1)。
那么g(n)/f(n)=[(2n-2)!/(n-1)!/(n-1)!]/[(2n)!/n!/n!/(n+1)]=n2(n+1)/(2n)/(2n-1)=n(n+1)/2(2n-1)。
于是一句话就做完了。
#include#include #include #include #include #include using namespace std;int read(){ int x=0,f=1;char c=getchar(); while (c<'0'||c>'9') { if (c=='-') f=-1;c=getchar();} while (c>='0'&&c<='9') x=(x<<1)+(x<<3)+(c^48),c=getchar(); return x*f;}double n;int main(){#ifndef ONLINE_JUDGE freopen("bzoj4001.in","r",stdin); freopen("bzoj4001.out","w",stdout); const char LL[]="%I64d";#else const char LL[]="%lld";#endif n=read(); printf("%.9lf",n*(n+1)/2/(2*n-1)); return 0;}